Chapter 12: IF Statements

Overview

• If I order up to 500 units of a product, I pay $3.00 per unit. If I order between 501 and 1200 units, I pay $2.70 per unit. If I order between 1201 and 2000 units, I pay $2.30 per unit. If I order more than 2000 units, I pay $2.00 per unit. How can I write a formula that expresses the purchase cost as a function of the number of units purchased?
• I've just purchased 100 shares of stock at a cost of $55 per share. To hedge the risk that the stock might decline in value, I purchased 60 six-month European put options. Each option has an exercise price of $45 and costs $5. How can I develop a spreadsheet that indicates the six-month percentage return on my portfolio for a variety of possible future prices?
• Many stock market analysts believe that moving-average trading rules can outperform the market. A commonly suggested movingaverage trading rule is to buy a stock when the stock's price moves above the average of the last 15 months and to sell a stock when the stock's price moves below the average of the last 15 months' price. How would this trading rule have performed against buying and holding the Standard and Poor's Index?
• In the game of craps, two dice are tossed. If the total of the dice on the first roll is 2, 3, or 12, you lose. If the total of the dice on the first roll is 7 or 11, you win. Otherwise, the game keeps going. How can I write a formula to determine the status of the game after the first roll?
• In most pro forma financial statements, cash is used as the plug to make assets and liabilities balance. I know that using debt as the plug would be more realistic. How can I set up a pro forma statement having debt as the plug?

The five situations listed above seem to have little, if anything, in common.-However, setting up Excel models for each of these situations requires the use of an IF statement. I believe that the IF formula is the single most useful formula in Excel. IF formulas let you conduct conditional tests on values and formulas, mimicking (to a limited degree) the conditional logic provided by computing languages such as C, C++, and Java. 

An IF formula begins with a condition, for example, A1>10. If the condition-is true, the formula returns the first value listed in the formula; otherwise, we move on within the formula and repeat the process. The easiest way to show you the power and utility of IF formulas is to use them to help answer each of our five questions. 

If I order up to 500 units of a product, I pay $3.00 per unit. If I order between 501 and 1200 units, I pay $2.70 per unit. If I order between 1201 and 2000 units, I pay $2.30 per unit. If I order more than 2000 units, I pay $2.00 per unit. How can I write a formula that expresses the purchase cost as a function of the number of units purchased?

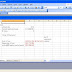
You can find the solution to this question on the worksheet named Quantity Discount in the file IfStatement.xls. The worksheet is shown in Figure 12-1.

Figure 12-1: You can use an IF formula to model quantity discounts. 

Suppose cell A9 contains our order quantity. We can compute an order's cost as a function of the order quantity by implementing the following logic:

• If A9<=500, the cost is 3*A9.
• If A9 is between 501 and 1200, the cost is 2.70*A9.
• If A9 is between 1201 and 2000, the cost is 2.30*A9.
• If A9 is more than 2000, the cost is 2*A9.

We begin by linking the range names in A2:A4 to cells B2:B4, and linking the range names in cells D2:D5 to cells C2:C5. We can implement this logic in cell B9 with the formula:

IF(A9<=cut1,price1*A9,IF(A9<=cut2,price2*A9,IF(A9<=cut3,price3*A9,price4*A9))) 

To understand how Excel computes a value from this formula, recall that IF statements are evaluated from left to right. If the order quantity is less than or equal to 500 ( cut1), the cost is given by price1*A9. If the order quantity is not less than 500, the formula checks to see whether the order quantity is less than 1200. If this is the case, the order quantity is between 501 and 1200, and the formula computes a cost of price2*A9. Next we check whether the order quantity is less than or equal to 2000. If this is true, the order quantity is between 1201 and 2000, and our formula computes a cost of price3*A9. Finally, if the order cost has not yet been computed, our formula defaults to the value price4*A9. In each case, the IF formula returns the correct order cost. Note that I typed in three more order quantities in cells A10:A12 and copied our cost formula to B10:B12. For each order quantity, our formula returns the correct total cost. 

An IF formula containing more than one IF statement is called a nested IF formula. A nested IF formula can contain up to seven IF statements and up to 256 characters. More complex formulas need to be broken into multiple cells. 

I've just purchased 100 shares of stock at a cost of $55 per share. To hedge the risk that the stock might decline in value, I purchased 60 six-month European put options. Each option has an exercise price of $45 and costs $5. How can I develop a spreadsheet that indicates the six-month percentage return on my portfolio for a variety of possible future prices? 

Before tackling this problem, I want to review some basic concepts from the world of finance. A European option allows you to sell at a given time in the future (in this case six months) a share of a stock for the exercise price (in this case $45). If our stock's price in 6 months is $45 or higher, the option has no value. Suppose, however, that the price of the stock in 6 months is below $45. Then you can make money by buying a share and immediately reselling the stock for $45. For example, if in 6 months our stock is selling for $37, you can make a profit of $45 - $37, or $8 per share, by buying a share for $37 and then using the put to resell the share for $45. You can see that put options protect you against downward moves in a stock price. In this case, whenever the stock's price in six months is below $45, the puts start kicking in some value. This cushions a portfolio against a decrease in value of the shares it owns. Note also that the percentage return on a portfolio is computed by taking the change in the portfolio's value ( final portfolio value - initial portfolio value) and dividing that number by the portfolio's initial value.

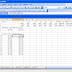
With this background, let's look at how the six-month percentage return on our portfolio, consisting of 60 puts and 100 shares of our stock, varies as the share price varies between $20 and $65. You can find this solution on the sheet named Hedging in the file IfStatement.xls. The worksheet is shown in Figure 12-2. 

Figure 12-2: Hedging example that uses IF statements. 

The labels in A2:A7 are linked to the cells B2:B7. The initial portfolio value is equal to 100($55) + 60($5) = $5,800, shown in cell B7. By copying from B9 to B10:B18 the formula IF(A9<exprice,exprice-A9,0)*Nputs, we compute the final value of our puts. If the six-month price is less than our exercise price, we value each put as exercise price-six-month price. Otherwise, each put will in six months have a value of $0. Copying from C9 to C10:C18 the formula Nshares*A9, we compute the final value of our shares. Copying from D9 to D10:D18 the formula ((C9+B9)-startvalue)/startvalue) computes the percentage return on our hedged portfolio. Copying from E9 to E10:E18 the formula (C9-Nshares*pricenow)/(Nshares*pricenow) computes the percentage return on our portfolio if we are unhedged (that is, buy no puts). 

In Figure 12-2, you can see that if the stock price drops below $45, our hedged portfolio has a larger expected return than our unhedged portfolio. Also note that if the stock price does not decrease, the unhedged portfolio has a larger expected return. This is why the purchase of puts is often referred to as portfolio insurance. 

Many stock market analysts believe that moving-average trading rules can outperform the market. A commonly suggested moving-average trading rule is to buy a stock when the stock's price moves above the average of the last 15 months and to sell a stock when the stock's price moves below the average of the last 15 months' price. How would this trading rule have performed against buying and holding the Standard and Poor's Index? 

In this example, we'll compare the performance of the moving-average trading rule (in the absence of transaction costs for buying and selling stock) to a buyand-hold strategy. The strength of a moving-average trading rule is that it helps you follow market trends. A moving-average trading rule lets you ride up with a bull market and sell before a bear market destroys you. Our data set contains the monthly value of the Standard and Poor's (S&P) Index for the time period January 1871 through October 2002. To track the performance of our movingaverage trading strategy, we need to track the following information each month:

• The average of the S&P Index over the last 15 months.
• Do we own stock at the beginning of each month?
• Do we buy stock during the month?
• Do we sell stock during the month?
• What is our cash flow for the month (positive if we sell stock, negative if we buy stock, and 0 otherwise)?

The file MaTradingRule.xls, shown in Figure 12-3, includes the work I did to answer this question. Tackling this problem requires several IF formulas, and some of the IF formulas will require an AND operator. For example, we'll buy the stock during a month if and only if we don't own the stock at the beginning of the month and the current month's price is larger than the 15-month moving average for the stock's price. The first month for which we can compute a 15-month moving average is April 1872, so we begin our calculations in row 24. 

Figure 12-3: Moving-average trading rule beats buy and hold! 

Tip

An easy way to copy the formula from D24 to D25:D1590 is to point at the lower right corner of cell D24 (the pointer is displayed as a crosshair) and then double-click the left mouse button. Double-clicking copies the formula in a column to match the number of filled rows in the column to the left of the current column. This trick can also be used to copy formulas in multiple columns.

• Let's assume we first owned the stock in April 1872, so we entered Yes in cell C24.
• By copying from D24 to D25:D1590 the formula AVERAGE(B9:B23), we compute the 15-month moving average for each month.
• By copying from E24 to E25:E1590 the formula IF(AND(C24="No", B24>D24),"yes","no"), we determine for each month whether our S&P share is purchased during the month. Remember that we purchase the share only if we did not own the stock at the beginning of the month and the current value of the S&P exceeds its 15-month moving average. Notice the AND portion of the formula. It contains two conditions (more than two are allowed) separated by a comma. If both conditions are satisfied, the formula returns Yes; otherwise, it returns No. For an IF formula to recognize text, you need to place quotation marks (' ') around the text.
• By copying from F24 to F25:F1590 the formula IF(AND(C24="Yes", B24<D24),"yes","no"), we determine for each month whether our S&P share is sold. The stock is sold if and only if we owned the S&P share at the beginning of the month and the current value of the S&P share is below the 15-month moving average. April 1873 is the first month in which we sell our S&P stock.
• During any month before October 2002, if we buy a share of the S&P during the month, our cash flow is negative the value of the S&P share we bought. If we sell a share of the S&P during the month, our cash flow equals the value of the S&P. Otherwise, the cash flow is 0. During October 2002, we sell any S&P share we own to get credit for its value. Therefore, by copying from G24 to G25:G1589 the formula IF(E24="yes",-B24,IF(F24="yes",B24,0)), we record our cash flow for all months before October 2002. Entering in cell G1590 the formula IF(C1590="yes",B1590,0) gives us credit for selling any stock we own at the beginning of October 2002.
• In cell G6 we compute our total profit from the moving-average trading strategy with the formula SUM(G24:G1590). We find the 15-month moving average strategy earns a profit of $1319.75.
• The profit from buying and holding shares is simply the October 2002 S&P value minus the April 1872 S&P value. We compute the profit from the buy-and-hold strategy in cell G7 with the formula B1590-B24. We find that the buy and hold profit of $849.45 is far worse than the profit from the moving-average trading rule.

In the game of craps, two dice are tossed. If the total of the dice on the first roll is 2, 3, or 12, you lose. If the total of the dice on the first roll is 7 or 11, you win. Otherwise, the game keeps going. How can I write a formula to determine the status of the game after the first roll? 

The fact that you lose in craps if you throw a 2, 3, or 12 can be conveniently modeled by placing an OR formula within an IF formula. In cell B5 of the worksheet Craps, shown in Figure 12-4 and found in the file IfStatement.xls, we enter the formula

IF(OR(A5=2,A5=3,A5=12),"Lose",IF(OR(A5=7,A5=11),"Win","Keep going")). This formula is then copied from B5 to B6:B7. The formula displays Lose if a 2, 3, or 12 is entered in cell A5. It displays Win if a 7 or 11 is entered, and it displays Keep going for any other value.

Figure 12-4: Using IF statements to model the first roll in craps. 

In most pro forma financial statements, cash is used as the plug to make assets and liabilities balance. I know that using debt as the plug would be more realistic. How can I set up a pro forma statement having debt as the plug? 

A pro forma is basically a prediction of a company's financial future. A pro forma requires construction of a company's future balance sheets and income statements. The balance sheet provides a snapshot of the company's assets and liabilities at any point in time. An income statement tells us how the company's financial status is changing at any point in time. Pro forma statements can help a company determine its future needs for debt and are also key parts of valuation models that stock analysts use to determine whether a stock is properly valued. In the file Proforma.xls, I've generated the free cash flows (FCFs) for the next four years for a firm. Figure 12-5 shows the balance sheet, and Figure 12-6 shows the income statement.

Figure 12-5: Pro forma assumptions and balance sheet.  

Figure 12-6: Pro forma income statement. 

Column D contains information about the company's current status (during-year 0). Our basic assumptions are as follows:

• Sales growth is 2 percent per year
• Initial sales are $1,000
• Interest rate on debt is 10 percent
• Dividend payout is 5 percent of net income
• The tax rate is 53 percent
• Cost of goods sold (COGS) are 75 percent of sales
• Depreciation is 10 percent of gross fixed assets
• Liquid assets earn 9 percent
• Current assets are 15 percent of sales
• Current liabilities are 7 percent of sales
• Net fixed assets are 60 percent of sales

I've assigned the names in the cell range C3:C10 to the cells in the range D3:D10. Then, during each year t, basic finance and accounting imply the following relationships, which are then implemented in a series of formulas.

• Year t+1 sales = (Year t sales)*(1+SG). I've computed sales during each year by copying from E28 to F28:H28 the formula D28*(1+SG). I'll refer to this formula as formula 12.1.
• Year t COGS = COGS*(Year t sales). Each year's COGS are computed by copying from E29 to F29:H29 the formula COGS*E28. I'll refer to this formula as 12.2.
• If Year t assets>Year t liabilities, Year t debt must be set equal to Year t total assets - Year t current liabilities - Year t equity. Otherwise, Year t debt = 0. I've computed each year's debt in E21:H21 with the formula IF((E18>E20+E24,E18-E20-E24,0). If Year t total assets are greater than Year t total liabilities, this formula sets Year t debt to Year t total assets - Year t current liabilities - Year t equity. This equalizes, or balances, assets and liabilities. Otherwise, we set Year t debt equal to 0. In this case, Year t cash and marketable securities will be used to balance assets and liabilities. (12.3)
• Year t current liabilities = (CL/Sales ratio)*(Year t sales). In E20:H20, we use the formula $H$4*E28 (formula 12.4) to compute current liabilities for each year (copying this formula from E20 to F20:H20).
• Year t equity = Year t stock + Year t retained earnings. In E24:H24, we compute equity by copying from E24 to F24:H24 the formula SUM(E22:E23). (12.5)
• If Year t debt is greater than 0, Year t cash and marketable securities equals 0. Otherwise, Year t cash and marketable securities equals MAX(0, Year t total liabilities - Year t current assets - Year t net fixed assets). In E13:H13, I compute cash and marketable securities for each year by copying from E13 to F13: H13 the formula IF(E21>0,0,MAX(0,E25-E14-E17)). If Year t debt is greater than 0, we need not use Year t cash and marketable securities to balance assets and liabilities. In this case we set Year t cash and marketable securities equal to 0. Otherwise, we set Year t cash and marketable securities equal to Year t total assets - Year t current liabilities - Year t equity. This balances assets and liabilities if Year t assets (without cash and marketable securities) are less than Year t liabilities. If debt does not balance assets and liabilities, this creates liquid assets as the plug that does balance assets and liabilities. (12.6)
• Year t interest expense = (Year t Debt)*IRD. In E33:H33, I compute interest expense by using the formula IRD*E21, copying this formula again to F33:H33. (12.7)

Year t interest income = (Year t cash and marketable securities)*LAIR.

In E32:H32, I compute interest income by copying from E32 to F32:H32 the formula LAIR*E13. (12.8)

• Year t operating income = Year t sales - Year t COGS - Year t depreciation. In E31:H31, operating income is computed by copying from E31 to F31:H31 the formula E28-E29-E30. (12.9)
• Year t dividends = (Year t net income)*DIV. In E39:H39, I copy from

E39 to F39:H39 the formula E36*DIV to compute dividends for each year. (12.10)

• Year t + 1 beginning retained earnings = Year t ending retained earnings. I compute beginning retained earnings each year in F38:H38, copying from F38 to G38:H38 the formula E40. (12.11)
• Year t end of year retained earnings = Year t beginning retained earnings + Year t net income - Year t dividends. In E40:H40, I compute each year's ending retained earnings by copying from E40 to F40:H40 the formula E38+E36-E39. (12.12)
• Year t income before taxes = Year t operating income - Year t interest expense + Year t cash income. By copying from E34 to F34:H34 the formula E31-E33+E32, I compute income before taxes. (12.13)
• Year t taxes = (Year t income before taxes)*TR. I compute each year's taxes in E35:H35 by copying from E35 to F35:H35 the formula TR*E34. (12.14)
• Year t net income after taxes = (Year t income before taxes) - (Year t taxes). In E36:H36, I compute each year's net income by copying from E36 to F36:H36 the formula E34-E35. (12.15)
• Year t net fixed assets = (Year t sales)*(NFA/Sales). In E17:H17, I compute each year's net fixed assets by copying the formula $H$5*E28 from E17 to F17:H17. (12.16)
• Year t gross fixed assets = Year t net fixed assets + Year t accumulated depreciation. In cells E15:H15, I compute gross fixed assets for each year by copying the formula E17+E16. (12.17)
• Year t depreciation = (Year t net fixed assets)*DEP. Each year I use the formula DEP*E15 to compute depreciation, copying the formula from E30 to F30:H30. (12.18)
• Year t accumulated depreciation = Year t-1 accumulated depreciation + Year t depreciation. Each year I use the formula D16+E30 to compute accumulated depreciation by copying the formula from E16 to F16:H16. (12.19)
• Year t net fixed assets = Year t gross fixed assets - Year t accumulated depreciation. In row 17, to compute net fixed assets, I copy from E16 to F16:H16 the formula D15-D16. (12.20)
• Year t total assets = Year t liquid assets + Year t net fixed assets + Year t cash and marketable securities. By adding liquid assets, current assets, and net fixed assets, I compute our total assets by copying from E18 to F18:H18 the formula SUM(E13,E14,E17). (12.21)
• Year t total liabilities = Year t current liabilities + Year t debt + Year t equity. By copying from E25 to F25: H25 the formula SUM(E20,E21,E24), I compute total liabilities for each period. Each year will balance because of our debt and liquid asset statements.

Formulas 12.3 and 12.6 require the use of IF statements. This spreadsheet will also contain circular references. (For more information about solving circular references, see Chapter 11). For example, the following relationships create a circular reference:

• Year t cash affects Year t total assets.
• Year t total assets affect Year t debt.
• Year t debt affects Year t cash.

For this spreadsheet to return sensible results, we need to select the Iteration-option on the Calculation tab of the Options dialog box. (Click Tools, Options to open the dialog box.) Note that for each year t, total assets in row 18 equal total liabilities in row 25. This shows the power of IF formulas and circular references