Overview
- How do I use NPV to compare the merits of investments for which cash flows are received at several points in time?
- How do I use the Excel NPV function?
- How can I compute NPV when cash flows are received at the beginning of a year or in the middle of the year?
- How can I compute NPV when cash flows are received at irregular intervals?
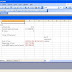
Consider the following two investments, whose cash flows are listed in the file NPVExample.xls and shown in Figure 8-1.
Figure 8-1: To determine which investment is better, we need to calculate net present value.
- Investment 1 requires a cash outflow of $10,000 today and a cash outflow of $14,000 two years from now. One year from now, investment 1 yields $24,000.
Which is the better investment? Investment 1 yields total cash inflow of $0, while investment 2 yields a total cash flow of $1,000. At first glance, investment 2 appears to be better. But wait a minute. Most of the cash outflow for investment 1 occurs two years from now, while most of the cash outflow for investment 2 occurs today. Spending $1.00 two years from now doesn't seem as costly as spending $1.00 today, so maybe investment 1 is better than it first appears. To determine which investment is better, we need to compare the values of cash flows received at different points in time. That's where the concept of net present value proves useful.
What is net present value?
The net present value (NPV) of a stream of cash flows received at different points in time is simply the value measured in today's dollars of the stream of cash flows. Suppose we have $1.00 today and we invest this dollar at an annual interest rate of r percent. This dollar will grow to 1 + r dollars in the first year, (1+r)2 in two years, and so on. We can say in some sense that $1 now equals $(1+r) a year from now and $(1+r)2 two years from now. In general, we can say that $1 now is equal to $(1+r)n n years from now. As an equation, we can express this calculation as follows:
$1now = $(1+r)n received n years from now
If we divide both sides of this equation by (1+r)n, we get the following important result:
This result tells us how to compute (in today's dollars) the NPV of any sequence of cash flows. You can convert any cash flow to today's dollars by multiplying the cash flow received n years from now ( n can be a fraction) by
You then add up the value of the cash flows (in today's dollars) to find the investment's NPV. Let's assume r is equal to 0.2. We could calculate the NPV for the two investments we're considering as follows:
On the basis of NPV, investment 1 is superior to investment 2. Although total cash flow for investment 2 exceeds total cash flow for investment 1, investment 1 has a better NPV because a greater proportion of investment 1's negative cash flow comes later and the NPV criterion gives less weight to cash flows that come later. If we use a value of .02 for r, investment 2 has a larger NPV because when r is very small, later cash flows are not discounted as much and NPV returns results similar to those derived by ranking investments according to total cash flow.
| Note | I made up the interest rate r =0.2, skirting the issue of how to determine an appropriate value of r. You would need to study finance for at least a year to understand the issues involved in determining an appropriate value for r. The appropriate value of r used to compute NPV is often called the company's cost of capital. Suffice it to say that most U.S. companies use an annual cost of capital between 0.1 (10 percent) and 0.2 (20 percent). If the annual interest rate is chosen according to accepted finance practices, projects with NPV>0 increase the value of a firm, projects with NPV<0 decrease the value of a firm, and projects with NPV=0 keep the value of a firm unchanged. A firm should (if it had unlimited investment capital) invest in every available investment having positive NPV. |
To determine the NPV of investment 1 in Excel, I first assigned the range name r_ to the interest rate (located in cell C3). I then copied the Time 0 cash flow from C5 to C7. I determined the NPV for investment 1's year 1 and year 2 cash flow by copying from D7 to E7 the formula D5/(1+r_)^D$4. (The symbol ^, located over the number 6 on the keyboard, raises a number to a power.) In cell A5, I computed the NPV of investment 1 by adding the NPV of each year's cash flow with the formula SUM(C7:E7). To determine the NPV for investment 2, I copied the formulas from C7:E7 to C8:E8 and copied the formula from A5 to A6.
How do I use the Excel NPV function?
The Excel NPV function uses the syntax NPV(rate, range of cells). Given a rate, the function determines the NPV for the given rate of the cash flows in the range of cells. The function's calculation assumes that the first cash flow is one period from now. In other words, entering the formula NPV(r_,C5:E5) will not determine the NPV for investment 1. Instead, this formula (entered in cell C14) computes the NPV of the following sequence of cash flows: -$10,000 a year from now, $24,000 two years from now, and -$14,000 three years from now. Let's call this investment 3. The NPV of investment 3 is $231.48. To compute the actual cash NPV of investment 1, I entered in cell C11 the formula C7+NPV(r_,D5:E5). This formula does not discount the Time 0 cash flow at all (which is correct because Time 0 cash flow is already in today's dollars), multiplies the cash flow in D5 by
and then multiplies the cash flow in E5 byThe formula in cell C11 yields the correct NPV of investment 1, $277.78.
How can I compute NPV when cash flows are received at the beginning of a year or in the middle of the year?
To use the NPV function to compute the net present value of a project whose cash flows always occur at the beginning of a year, you can use the approach we followed to determine the NPV of investment 1: separate out the year 1 cash flow and apply the NPV function to the remaining cash flows. Alternatively, observe that for any year n, $1 received at the beginning of year n is equivalent to $(1+r) received at the end of year n. Remember that in one year, a dollar will grow by a factor (1+r).
Thus, if we multiply the result obtained with the NPV function by (1+r), we can convert the NPV of a sequence of end-of-year cash flows to the NPV of a sequence of cash flows received at the beginning of the year. We can also compute the NPV of investment 1 in cell D11 with the formula (1+r_)*C14.
Of course, we again obtain an NPV of $277.78.
Now suppose the cash flows for an investment occur in the middle of each year. For an organization such as MSN, which receives monthly subscription revenue, we can approximate the 12 monthly revenues received during a given year as a lump sum received in the middle of the year. How can we use the NPV function to determine the NPV of a sequence of mid-year cash flows? For any year n,
received at the end of year n is equivalent to $1 received at the middle of year n because in half a year $1 will grow by a factor of
If we assume the cash flows for investment 1 occur mid year, we can compute the NPV of the mid-year version of investment 1 in cell C17 with the formula SQRT(1+r_)*C14. We obtain a value of $253.58.
How can I compute NPV when cash flows are received at irregular intervals?
Cash flows often occur at irregular intervals, which makes computing the NPV or internal rate of return (IRR) of these cash flows more difficult. Fortunately, the Excel XNPV function makes computing the NPV of irregularly timed cash flows a snap.
| Note | To use the XNPV function, you need to first install the Analysis Toolpak. To install the Analysis Toolpak, select Tools, Add-Ins and then check the options for the Analysis Toolpak and Analysis Toolpak VBA. |
The XNPV function uses the syntax XNPV(rate,values,dates). The first date listed must be the earliest. Other dates need not be listed in chronological order. The XNPV function computes the NPV of the given cash flows assuming the current date is the first date in the sequence. For example, if the first listed date is 2/15/03, the NPV is computed in February 15, 2003, dollars.
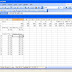
To illustrate the use of the XNPV function, look at the example on Sheet 1 in the file XNPV.xls, which is shown in Figure 8-2. Suppose that on 4/08/01 we paid out $900. Later we receive the following amounts:
- $300 on 8/15/01
- $200 on 6/25/02
- $100 on 7/03/03
If the annual interest rate is 10 percent, what is the NPV of these cash flows? We enter the dates (in Excel date format) in D3:D7 and the cash flows in E3:E7. Entering the formula XNPV(A9,E3:E7,D3:D7) in cell D11 computes the project's NPV in 4/08/01 dollars because 4/08/01 is the first date listed. This project would have an NPV, in 4/8/2001 dollars, of $20.63.
Figure 8-2: XNPV function example.
The computations performed by the XNPV function are as follows:
- Compute the number of years after April 8, 2001, that each date occurred. (We did this in column F.) For example, 8/15/01 is .3534 years after 04/08/01.
- Discount cash flows at the rateFor example, the 8/15/2001 cash flow is discounted by
Suppose that today's date is actually 2/14/01. How would you compute the NPV of an investment in today's dollars? Simply add a row with today's date and 0 cash flow and include this row in the range for the XNPV function. (See Figure 8-3 and the worksheet Today.) The NPV of the project in today's dollars is $20.34.
Figure 8-3: NPV converted to today's dollars.
4. Use the XNPV function to obtain an exact answer to problem 3.
5. Consider the following set of cash flows over a four-year period:
Year | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
($600.00) | $550.00 | ($680.00) | $1,000.00 |
Determine the NPV of these cash flows if r = .15 and cash flows occur at the end of the year.
6. Solve problem 5 assuming cash flows occur at the beginning of each year.
7. Consider the following cash flows:
Date | Cash Flow |
|---|---|
12/15/01 | ($1,000.00) |
1/11/02 | $300.00 |
4/07/03 | $600.00 |
7/15/04 | $925.00 |
If today is November 1, 2001, and r = .15, what is the NPV of these cash flows?
8. After earning an MBA, a student will begin working at an $80,000-ayear job on September 1, 2005. She expects to receive a 5 percent raise each year until she retires on September 1, 2035. If the cost of capital is 8 percent a year, determine the total present value of her before tax earnings.













No comments:
Post a Comment