Chapter 10: Functions for Personal Financial Decisions: The PV, FV, PMT, PPMT, and IPMT Functions

Overview

• Should I pay $11,000 today for a copier or $3,000 a year for 5 years?
• If I invest $2,000 a year for 40 years toward my retirement and earn 8 percent a year on my investments, how much will I have when I retire?
• I am borrowing $10,000 on a 10-month loan with an annual interest rate of 8 percent. What will my monthly payments be? How much principal and interest am I paying each month?

When we borrow money to buy a car or a house, we always wonder whether we're getting a good deal. When we save for retirement, we're curious how large a nest egg we'll have when we retire. In our daily work and personal life, financial questions similar to these questions often arise. Knowing how to use the PV, FV, PMT, PPMT, and IPMT functions in Excel makes answering these types of questions easy. 

Should I pay $11,000 today for a copier or $3,000 a year for 5 years? 

The key to answering this question is attributing a value to the annual payments of $3,000 per year. Let's assume the cost of capital is 12 percent per year. We could use the NPV function to answer this question, but the PV function provides a much quicker means to solve this problem. (For more information about the NPV function, see Chapter 8.) 

The PV function returns the value in today's dollars of a series of future payments, assuming periodic, constant payments and a constant interest rate. A stream of cash flows that includes the same amount of cash outflow (or inflow) each period is called an annuity, and assuming that each period's interest rate is the same, an annuity can be valued using the PV function. Here's the syntax for the PV function: 

PV(rate,#per,[pmt],[fv],[type]) 

• Rate is the interest rate per period. If you borrow money at 6 percent per year and the period is a year, rate equals 0.06. If the period is a month, rate equals 0.06/12, or 0.005.
• #per is the number of periods in the annuity. In our copier example, #per equals 5. If payments for the copier are made each month for 5 years, #per equals 60. Your rate must be consistent with #per, of course. In other words, if #per implies that a period is a month, you need to use a monthly interest rate. If #per implies that a period is a year, use an annual interest rate.
• Pmt is the payment made each period. In our example, pmt is $5,000. A payment is a positive number, while money received is a negative number.
• Fv is the cash balance (or future value) that you want to have after the last payment is made. In our copier example, fv equals 0. (If we want a $5,000 cash balance after the last payment, fv would equal $5,000.) If fv is omitted, it's assumed to equal 0.
• Type is either 0 or 1. Type indicates when payments are made. If type is omitted or equal to 0, payments are made at the end of each period. When type equals 1, payments are made at the beginning of each period.

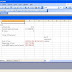
The solution to the question about the best way to pay for the copier is included in the file PV.xls, shown in Figure 10-1.

 

Figure 10-1: The PV function calculates the present value of payments. 

In cell D8, I computed the present value of paying $3,000 per year for 5 years (at the end of each year) with a 12 percent cost of capital. Here's the formula I used: 

PV(annual_rate,Years,Amount_paid_each_year,0,0) 

I named the cells D3:D5 with the labels in C3:C5 by using the Insert, Name Create command. (See Chapter 1 for information about creating range names.) Excel returns a net present value of -$10,814.33. (The negative sign means we are paying money out.) By omitting the last two arguments, I obtain the same answer in cell E8 with the formula 

PV(annual_rate,Years,Amount_paid_each_year) 

Making payments at the end of the year is a better deal than paying out $11,000 today.

To calculate the net present value of the payments if we make payments of $3,000 on the copier for 5 years at the beginning of each year, I used the formula in cell D9: 

PV(annual_rate,Years,Amount_paid_each_year,0,1) 

Changing the last argument from a 0 to a 1 changes the calculation, which is now based on payments at the beginning of the year rather than payments at the end of the year. With this change, the present value of the payments is $12,112.05, so it's better to pay $11,000 today than to make payments at the beginning of the year. 

Suppose we pay $3,000 at the end of each year and we have to include an extra $500 payment at the end of year 5. We can find the present value of all our payments by including a future value of $500, using the following formula: 

PV(annual_rate,Years,Amount_paid_each_year,500,0). 

In this calculation, the present value of the payments equals $11,098.04. 

If I invest $2,000 a year for 40 years toward my retirement and earn 8 percent a year on my investments, how much will I have when I retire? 

In this situation, we want to know the value of an annuity in future dollars (40 years from now) and not in today's dollars. This is a job for the FV or future value function. The future value function calculates the future value of an investment assuming periodic, constant payments with a constant interest rate. The syntax of the FV function is as follows: 

FV(rate,#per,[pmt],[pv],[type]) 

• Rate is the interest rate per period. In our example, rate is 0.08
• #per is the number of periods in the future at which you want to compute the future value. #per is also the number of periods during which the annuity payment is received. In our case, #per equals 40.
• Pmt is the payment made each period. In this example, pmt is -$2,000. The negative sign indicates we are receiving money.
• Pv is the amount of money (in today's dollars) owed right now. In our case, pv equals $0. If we owed someone $10,000 today, pv would equal $10,000. If we had $10,000 in the bank today, pv would equal -$10,000. If pv is omitted, it's assumed to equal zero.
• Type is 0 or 1, and it indicates when payments are due or money is deposited. If type equals 0 or is omitted, money is deposited at the end of a period. In our example, type is 0 or omitted. If type equals 1, payments are made or money is deposited at the beginning of a period.

The file FV.xls, shown in Figure 10-2, contains the resolution to this question.-In cell B7, I've entered the formula FV(Rate,Years,-Annual_deposit,0,0) to find that in 40 years our nest egg will be worth $518,113.04. Notice that I entered a negative value for our annual payment because a deposit can be viewed as a negative payment. In cell C7, I obtained the same answer by omitting the last two (unnecessary) arguments. The formula entered in C7 is FV(Rate,Years,-Annual_deposit). If deposits are made at the beginning of each year for 40 years, the formula entered in cell B8, which is FV(Rate,Years,Annual_deposit,0,1), yields the value of our nest egg in 40 years, $559,562.08. 

Figure 10-2: You can use the FV function to calculate the future value of investments. 

Finally, suppose that in addition to investing $2,000 at the end of each of the next 40 years, we have $30,000 with which to invest initially. If we earn 8 percent per year on our investments, how much money will we have when we retire in 40 years? We can answer this question by setting pv equal to -$30,000 in the FV function. (The negative sign indicates that we have money rather than owe someone money.) In cell B9 the formula 

FV(Rate,Years,-Annual_deposit,0,0)+FV(Rate,Years,0,-30000,1) 

yields a future value of $1,169,848.68. The formula FV(Rate,Years,0,-30000,1) yields the future value (in 40 years) of $30,000 received today. The formula includes type = 1 because $30,000 is received today. I used a negative sign with the $30,000 because we are 'owed' -$30,000. By the way, because our money is growing at 8 percent a year, FV(Rate,Years,0,-30000,1) simply yields (1.08)40($30,000). 

I am borrowing $10,000 on a 10-month loan with an annual interest rate of 8 percent. What will my monthly payments be? How much principal and interest am I paying each month? 

The Excel PMT function computes the periodic payments for a loan, assuming constant payments and a constant interest rate. The syntax of the PMT function is 

PMT(rate,#per,pv,[fv],[type]) 

• Rate is the per-period interest rate on the loan. In our example, we'll use one month as a period, so rate = 0.08/12, or 0.006666667.
• #per is the number of payments made. In our case, #per = 10.
• Pv is the present value of all our payments. That is, pv is the amount of the loan. In our case, pv equals $10,000.
• Fv is an optional argument that indicates the cash balance you want after making the last payment. In our case, fv is 0. If fv is omitted, Excel assumes it is 0. If you want to have all but $1,000 of the loan paid off at the end of 10 months, fv would equal -1,000.
• Type is 0 or 1 and indicates when payments are due. If type equals 0 or is omitted, payments are made at the end of the period. In this example, we'll first assume end of month payment. If type is 1, payments are made (or money deposited) at beginning of the period.

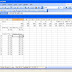
You can find an example of the PMT function in the file PMT.xls, shown in Figure 10-3. In cell G1, I computed the monthly payment on a 10-month loan for $10,000, assuming an 8 percent annual rate and end-of-month payments. The formula is:

PMT(rate,months,loan_amount) 

Figure 10-3: Examples of the PMT, PPMT, and IPMT functions. 

(Note that I used the names in cell range D1:D3 for the cell range E1:E3.) The monthly payment is $1,037.03. If you want, you can use the IPMT or the PPMT function to compute the amount of interest paid each month toward the loan and the amount of the balance paid down each month (called the payment on the principal). 

To determine the interest paid each month, use the IPMT function. The syntax of the function is: 

IPMT(rate, per, #per, pv, [fv],[type]) 

Except for the per argument, the arguments for the IPMT function are the same as for the PMT function. The per argument indicates the period number for which you're computing the interest.

Similarly, to determine the amount paid toward the principal each month, use the PPMT function. The syntax of the PPMT function is: 

 

PPMT( rate, per, #per, pv, fv, type) 

The meaning of each argument is the same as for the IPMT function.

By copying from F6 to F7:F15 the formula 

-PPMT(rate,C6,months,loan_amount) 

I compute each month's payment toward the principal. For example, during month 1, only $970.37 is paid toward principal. (As expected, the amount paid toward principal increases each month.) The minus sign is needed in the formula because Excel's natural convention is to label a payment as negative. 

By copying from G6 to G7:G15 the formula  

-IPMT(rate,C6,months,loan_amount)

I compute the amount of interest paid each month. For example, in month 1 we pay $66.67 in interest. Of course, the amount of interest we pay each month decreases. Note that each month (Interest Paid) + (Payment Toward Principal) = (Total Payment). Sometimes the total is off by a penny because of rounding. 

I can also create ending balances for each month in column H by using the relationship (Ending Month t Balance) = (Beginning Month t Balance) - (Month t Payment toward Principal).

With a beginning balance of $10,000 in month 1, we create each month's beginning balance in column D by using the relationship (Beginning Month t Balance) = (Ending Month t-1 Balance), where t = 2, 3, and so on up to 10. Of course, at the end of month 10, the balance is $0, as we'd expect. 

Our interest each month can be computed as follows:

(Month t Interest) = (Interest rate)*(Beginning Month t Balance) 

For example, for month 3 the interest is (0.0066667)*($8,052.80) = $53.69. Note, of course, that the net present value of all our payments is exactly $10,000. We checked this in cell D17 by using the formula NPV(rate,E6:E15). (See Figure 10-4.) 

Figure 10-4: Calculations that use the PMT function to show payment amounts that occur at beginning of a month or with an ending balance. 

If we make payments at the beginning of each month, the amount of each payment is computed in cell D19 with the formula: 

PMT(rate,months,loan_amount,0,1) 

Changing the last argument to 1 changes the timing of each payment to the beginning of the month. Because our lender is getting her money earlier, our monthly payments are less than in the end-of-the-month case. If we pay at the beginning of the month, our monthly payment is $1,030.16.

Finally, suppose that we want to leave $1,000 of our loan balance unpaid at the end of 10 months. If we make payments at the end of the month, the formula PMT(rate,months,loan_amount,-1000), entered in cell D20, computes our monthly payment. Our monthly payment turns out to be $940.00. Because we are leaving $1,000 of our balance unpaid, it makes sense that our new monthly payment is less than the original end-of-month payment, $1,037.03.